Математика. 5-6 классы: поурочные планы по учебникам Н. Я. Виленкина, В.И. Жохова, А.С. Чеснокова, С.И. Шварцбурда. Программа для установки через Интернет
| Код | СИ-108.4 |
| Авторы-составители | Афанасьева Т. Л., Пожарская О. В., Стромова З. С., Тапилина Л. А. |
| Издательство | Учитель, 2022 |
| Серия | Поурочное планирование |
| Электронная версия | скачать |
Инструкция по оплате и установке электронной продукции через Интернет: ознакомиться.
Покупка одного экземпляра программы дает право её использования на одном ПК.
1. Математика. 5 класс: учебник для общеобразовательных учреждений / Н. Я. Виленкин и др. - М.: Мнемозина, 2010.
2. Математика. 6 класс: учебник для общеобразовательных учреждений / Н. Я. Виленкин и др. - М.: Мнемозина, 2010.
Государственная программа по математике для общеобразовательных школ, гимназий, лицеев предусматривает для 5-6 классов два варианта учебного плана: 5 часов и 6 часов математики в неделю. Вашему вниманию предлагается поурочное планирование для 5-6 классов при пяти уроках в неделю (170 уроков в году).
В поурочном планировании предложена одна из возможных структур урока, позволяющая достаточно эффективно использовать учебное время, наиболее полно реализовать возможности содержания учебников, тем самым достигая высокого качества математических знаний у учащихся.
С этим товаром покупают
Примеры документов
Обозначение натуральных чисел. Урок 1
Урок № 3
Обозначение натуральных чисел (п. 1)
Цели: систематизировать и обобщить сведения о натуральных числах.
Оборудование: на доске нарисовать вычислительные цепочки.
Ход урока
I. Итоги предыдущего тестирования.
Анализ ошибок учащихся.
1. Вычислительные ошибки:
а) при вычитании чисел;
б) при умножении;
в) при делении.
2. Ошибки при определении порядка действий.
3. Ошибки на нахождение:
а) площади прямоугольника;
б) периметра квадрата;
4. Ошибки при нахождении времени движения, если известны скорость и расстояние.
II. Устные упражнения (на доске записаны вычислительные цепочки).
1. Выполните вычисления и заполните пропуски.
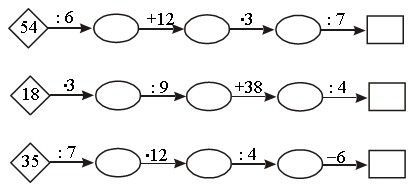
2. Из учебника решить № 14, 13, 16.
III. Изучение нового материала.
1. Как называются числа, которые мы сейчас складывали, вычитали, умножали и делили? (Натуральные числа.)
2. Для чего используют натуральные числа?
Учитель: Назовите самое маленькое натуральное число, самое большое натуральное число.
– Ученые считают, что люди научились считать 10 тысяч лет тому назад. Но овладение людьми все большими числами в истории человечества происходило долго и медленно. До сих пор путешественники находят иногда отсталые племена, которые не знают чисел, больших 10.
3. Сколько цифр использует человек, чтобы записать любое натуральное число? Назовите их.
4. Как называют запись чисел? (Десятичной.)
Учитель: Первобытный человек пользовался при счете предметов числом пальцев на двух руках – 10 пальцев. Отсюда и пошла десятичная система исчисления.
5. Рассмотрим числа: 234, 542, 471. Что обозначает цифра «4» в каждом числе?
6. Что обозначает каждая цифра в числе 537?
7 – разряд единиц, 3 – разряд десятков, 5 – разряд сотен.
7. Какая цифра означает отсутствие разряда?
Является ли нуль натуральным числом?
8. Сейчас мы научимся читать многозначные числа.
Пусть мы должны прочитать число: 385 647 409 129 (читается и обсуждается соответствующий обзац учебника).
9. Прочитать числа (на доске записаны заранее) 43 621 015 000, 57 241 346 189.
10. Рассмотреть таблицу на с. 6.
IV. Физкультминутка («истинно–ложно»).
Учитель: Я скажу несколько математических предложений. Если предположение верное, то вы сидите, если оно ложное, вы встаёте и кто-то из вас объясняет, почему ложное.
1. В записи числа «Одна тысяча» три нуля.
2. В записи числа «Один миллион» пять нулей.
3. Для записи натуральных чисел употребляются одиннадцать цифр.
4. Последующее натуральное число отличается от предыдущего на единицу.
5. В записи числа «Один миллиард» девять нулей.
6. Вам известно только три класса многозначных чисел.
V. Закрепление.
Решить № 1 (устно), № 2, 3, 4 (устно).
VI. Подвести итог урока.
Учитель: Что нового узнали на уроке? Чему научились?
VII. Домашнее задание.
П. 1, № 23–26. Записать в математический словарь: натуральные числа, миллион, миллиард.
Примечание.
Отрезок. Сравнение отрезков
Урок № 5
Отрезок. Сравнение отрезков (п. 2)
Цели: сформировать у учащихся понятие отрезка, научить строить отрезок, сравнивать отрезки.
Оборудование: циркуль, линейка, цветные мелки.
Ход урока
I. Подготовка к восприятию новой темы.
1. Повторить хором латинский алфавит (он дан на форзаце учебника).
2. Напомнить о технике безопасности пользования циркулем, треугольником.
II. Изучение нового материала.
Учитель объявляет тему урока, записывает её на доске, а учащиеся в тетрадях.
Одновременно выполняют работу учитель у доски, а учащиеся в своих тетрадях:
1. Возьмите произвольно две точки (изобразить синим мелом).
2. Обозначим их буквами С и F (названия букв желтым мелом).
3. Приложим линейку к точкам и проведем отрезок (проводится красным мелом).
4. Вопросы учителя: Как вы думаете, как эта фигура называется? Правильно, CF – отрезок (записывается на доске и в тетрадях).
Как называются точки С и F? (Обязательно кто-то из учеников догадается). Да, ты прав.
Запись: «С и F – концы отрезка CF».
5. Соединим точки С и F другими линиями.
Будут ли эти линии отрезками?
Ведь между двух соседних точек
Отрезок – самый краткий путь.
Иначе слишком много точек
Необходимо обогнуть.
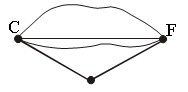
6. Сколькими отрезками можно соединить две точки? Этот вывод вы можете найти в учебнике на с. 10. Прочитайте его (несколько человек по очереди читают), запишите это в тетради.
7. Работа по учебнику.
а) Рассмотрите рис. 1. Какая фигура изображена на рисунке? Назовите концы этого отрезка.
б) Внимательно рассмотрите рис. 2. На нем изображен отрезок КМ. Чем отличается положение точки О и точки Е?
Говорят: «Точка Е лежит на отрезке КМ», «Точка Е принадлежит отрезку КМ», «Точка Е лежит между точками К и М», «Точка О не лежит на отрезке КМ», «Точка О не принадлежит отрезку КМ».
в) Что вы скажете про точку Р?
III. Физкультминутка.
1. Аккуратно положите свои инструменты, ручку.
2. Закройте глаза, очень сильно зажмурьтесь, откройте глаза. Проделайте это упражнение сами 6 раз.
3. Голову держите прямо, глаза подняли вверх, опустили вниз, посмотрели влево, посмотрели вправо (выполнить 6 раз).
4. Голову откиньте назад, опустите вперед так, чтобы подбородок упёрся в грудь (проделать 6 раз).
IV. Продолжение объяснения нового материала.
1. Учитель на доске чертит несколько различных отрезков, среди них есть равные, например АВ и MN.
2. При помощи циркуля убеждаемся, что отрезки равны, математически это записывается так, АВ = MN.
3. Работа с книгой: рис. 3. Выясняется, что отрезок ЕН короче отрезка EF (ЕН < EF), а отрезок EF длиннее отрезка ЕН (EF > EH).
V. Закрепление.
1. Выполнить № 30 (один ученик выполняет на доске, остальные в тетради).
2. Выполнить № 31, 32 (устно), № 34.
3. Выполнить № 52 (повторение пройденного).
VI. Итог урока.
1. Что нового узнали на уроке?
2. Учитель задает учащимся первые четыре вопроса (с. 12).
Шкалы
Урок № 9
Шкалы (п. 4)
Цели: сформировать понятие шкалы, деления шкалы, научить определять на шкале единичный отрезок, измерять при помощи приборов.
Оборудование: демонстрационная линейка, термометр, весы, часы; плакат.
Ход урока
I. Устные упражнения.
1. Исключите лишнее слово:
а) сумма, разность, множитель, частное.
б) девять, двенадцать, восемь, пятнадцать.
2. № 122 (1–3 строка), № 125, 126 (а), 131.
II. Изучение нового материала.
1. На линейке продемонстрировать и рассказать о штрихах, делениях, шкале.
2. Рассмотреть шкалу на своих линейках.
3. Прочитать соответствующий абзац в учебнике.
4. Вспомнить, какие ещё бывают шкалы (рассказать об устройстве термометра, о шкале на весах, циферблате на часах).
Дети могут сами сказать, что шкала есть на спидометрах, показателях количества бензина, транспортире.
5. Вспомните единицы измерения массы.
![]()
Можно сказать учащимся о миллиграммах.
III. Физкультминутка.
IV. Закрепление.
1. Какова цена одного деления на рисунке? (Плакат.)
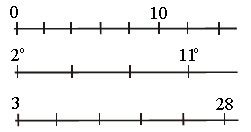
2. № 108 (а, б), 109, 110, 102 – устно; № 109 (выполнить на доске «в клеточку»).
3. № 113–115 учащиеся выполняют самостоятельно по образцу:
3 т 100 кг = 3100 кг, а затем обмениваются с соседом тетрадями и сверяют ответы с доской. (Ответы записаны на доске заранее.) Можно поставить оценку. (Нет ошибок – «5», одна ошибка – «4», две ошибки – «3», если ошибок больше двух, то «2»).
4. Решить задачи № 130, 132 (можно полуписьменно).
V. Итог урока.
1. С какими новыми математическими терминами мы познакомились? (Штрихи, деления, шкалы.)
2. Лена утверждает, что MN = 70 мм, АВ = 50 мм, а Толя думает, что MN = 7 см, АВ = 5 см. Кто из них прав, если каждому делению соответствует 5 мм?
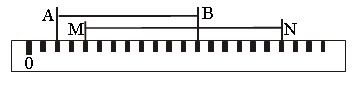
VI. Домашнее задание: п. 4 (с. 25), № 137, 139, 140, 144 (б).
Меньше или больше
Урок № 11
Меньше или больше (п. 5)
Цели: научить сравнивать натуральные числа: с одинаковым количеством цифр, с разным числом цифр.
Оборудование: плакат или кодоплёнка с устными упражнениями.
Ход урока
I. Устные упражнения.
1. Отгадать ребус. (Ребус – это загадка, в которой искомое слово изображено буквами, знаками, фигурами).

2. Найти координаты точек А, В, С, О.
![]()
3. Какая из точек на шкале изображена неверно?
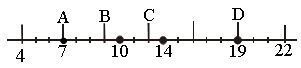
4. № 159 (а, б, в).
II. Изучение нового материала.
1. Сравнение натуральных чисел с использованием счета (читают и разбирают первый абзац).
2. Как узнать, левее или правее лежит одна точка относительно другой? (Прочитать второй абзац и рассмотреть рис. 28.)
3. Какой из этих абзацев нужно хорошо запомнить? (Второй.)
(Можно дать одну минуту для запоминания, попросить учеников закрыть учебник и проговорить хором.)
4. Объяснение учителя.
Результат сравнения записывают в виде неравенства.
«5 меньше 8»: 5 < 8; «12 больше 3»: 12 > 3.
«Число 7 больше 5 и меньше 10» записывается в виде двойного неравенства: 5 < 7 < 10.
(Обратить внимание на правильное чтение двойного неравенства.)
5. Работа по учебнику.
а) Сравнение многозначных чисел.
б) Как записывается результат сравнения отрезков?
III. Физкультминутка (упражнения для глаз).
1. Закрыть глаза, снять напряжение с плеч и в удобной позе отдохнуть одну минуту.
2. Точки под глазами слегка нажимают подушечками указательного и среднего пальцев, двигая ими по кругу одну минуту. Очень хорошо помогает.
IV. Закрепление.
1. № 145, 146 .
Можно организовать работу так: учитель говорит какое-либо высказывание. Например: «Точка А(1) левее точки В(8)». Если высказывание не верно, ученики поднимают руку. В некоторых случаях можно задать вопрос «Почему?».
2. № 147, 148. Сначала выясняют смысл задания, а затем решают с комментированием.
3. № 149, 150, 154 (устно).
4. Решить задачу самостоятельно.
Вариант I – № 166 (1), вариант II – № 166 (2).
(Для проверки на откидной доске показать правильное решение.)
V. Итог урока.
1. Прочитать неравенство 21 < 28 < 32.
2. Назвать натуральные числа, которые лежат между числами 3074 и 3081.
VI. Домашнее задание: п. 5, повторить п.п. 1–4, № 168, 169, 171, 172. В математический словарь занести слово «ребус».
Контрольная работа № 1
Урок № 14
Контрольная работа (п. 1–5)
Оборудование: карточки с текстом контрольной работы; карточки с дополнительными заданиями для тех, кто контрольную работу решил раньше.
Ход урока
Вариант I
1. Начертите отрезок МХ и отметьте на нём точку С. Измерьте отрезки МХ и СХ.
2. Постройте отрезок АВ = 6 см 2 мм и отметьте на нём точки D и С так, чтобы точка D лежала между точками С и В.
3. Отметьте точки Р и К и проведите луч КР. Начертите прямую МN, пересекающую луч КР, и прямую АВ, не пересекающую луч КР.
4. На координатном луче, единичный отрезок которого равен длине одной клетки тетради, отметьте точки М(3), Р(5), С(7) и N(10). На этом же луче отметьте точку Y, если её координата – натуральное число, которое меньше 10, но больше 8.
5. Запишите число, оканчивающееся цифрой 8, которое больше любого трёхзначного числа и меньше 1018.
Вариант II
1. Начертите отрезок МY и отметьте на нём точку D. Измерьте отрезки МD и DY.
2. Постройте отрезок DC = 3 см 4 мм и отметьте на нём точки А и В так, чтобы точка В лежала между точками D и А.
3. Отметьте точки M и N и проведите прямую MN. Начертите луч АВ, пересекающий эту прямую, и луч DC, не пересекающий её.
4. На координатном луче, единичный отрезок которого равен длине одной клетки тетради, отметьте точки С(4), D(6), Е(8) и F(11). На этом же луче отметьте точку М, если её координата – натуральное число, которое больше 11, но меньше 13.
5. Запишите число, оканчивающееся цифрой 7, зная, что оно меньше пятизначного числа и больше 9987.
Дополнительные задачи
Вариант I
Рассмотрите рисунок.
1. Заполните пропуски. На чертеже даны:
отрезки_________________;
лучи____________________;
прямые_________________.
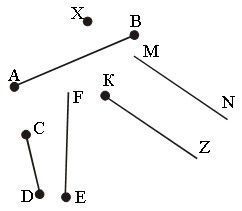
2. Запишите в кружке букву «И», если высказывание истинное, и букву «Л», если оно ложное. Если потребуется, то сделайте дополнительные построения.
а) Точка Х расположена на прямой MN. ![]()
б) Луч EF проходит через точку Х. ![]()
в) Точка Х принадлежит лучу KZ. ![]()
г) Точка Х расположена на отрезке CD. ![]()
Вариант II
Рассмотрите рисунок.
1. Заполните пропуски. На чертеже даны:
отрезки__________________;
лучи____________________;
прямые_________________.
Товар размещен в разделах
QR-код страницы
Для партнеров
с учмагом










